
In different cases, the objective function and constraints may be highly sensitive to these uncertainties which will lead to constrain violation or performance reduction. However, considering some degrees of uncertainty in characterizing any real engineering system is inevitable. 1270-9638/$ – see front matter © 2012 Elsevier Masson SAS. Traditional optimization methods which are applied in MDO problems generate optimal designs using deterministic designĬorresponding author. Many successful examples of MDO applications have been found in many fields, such as aerospace (aircraft, launch vehicle, satellite, etc.), automobile, electronic, and structures. It will allow system engineers to systematically explore the vast trade space in an intelligent manner and consider many more system architecture during the conceptual design phase before converging to the final design. Multidisciplinary Design Optimization (MDO) involves the coordination of multidisciplinary analyses to realize more effective solutions during the design and optimization of complex systems. A complex interrelation exists among mission trajectory, aerodynamics, propulsion, weight and structure with conflicting goals which have to be matched by an appropriate optimization strategy. Introduction The design of complex systems such as aerospace launch vehicles (ALVs) requires making appropriate compromises to achieve the optimal design among many coupled objectives such as high performance, safety, simplicity, ease of operation and low cost. Although the launch vehicle throw weight is increased negligibly in comparison with deterministic optimization, results show that the reliability-based method satisfied desired reliability of the constraints. Sequential Quadratic Programming (SQP) technique is used to achieve the optimal solution. Assuming a normal distribution for the uncertain variables, Latin Hypercube Sampling (LHS) method selects the sample values for simulation runs which are eventually utilized for calculating probability density function of constraints and their reliability at each design point. The constraints that appear during the flight are also considered.
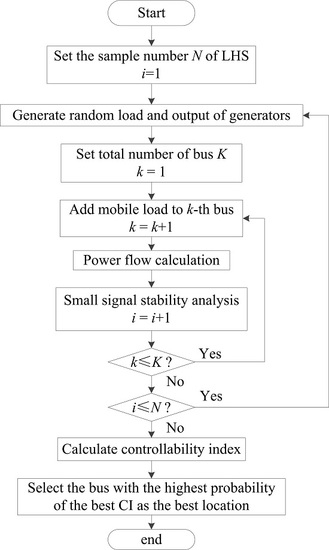
Mission constraints contain the final velocity, the height above ground, and flight path angle. Design variables for system level optimization are selected from propulsion, geometry and trajectory disciplines. Throw weight minimization is chosen as objective function.
Propulsion, weight, aerodynamics (geometry) and trajectory (performance) disciplines are used in an appropriate combination. Toosi University of Technology, East Vafadar Bld., 4th Tehranpars Sq., Postal Code: 16569-83911, Tehran, IranĪrticle history: Received 20 March 2012 Received in revised form 15 October 2012 Accepted 29 November 2012 Available online 12 December 2012 Keywords: Multidisciplinary design optimization Reliability-based design Latin hypercube sampling Solid propellant launch vehicleĪ b s t r a c t In this paper, Reliability-Based Multidisciplinary Design Optimization (RBMDO) of a two-stage solid propellant expendable launch vehicle (LV) is investigated. Aerospace Science and Technology 28 (2013) 297–304Ĭontents lists available at SciVerse ScienceDirectĪerospace Science and Technology Latin hypercube sampling applied to reliability-based multidisciplinary design optimization of a launch vehicle Jafar Roshanian 1, Masoud Ebrahimi ∗,2 Faculty of Aerospace Engineering, K.N.


 0 kommentar(er)
0 kommentar(er)
